-

—А—Г—Б—Б–Ї–Є–є

- sales@vrvibratory.com
–°–≤—П–ґ–Є—В–µ—Б—М —Б –љ–∞–Љ–Є –њ–Њ —Н–ї–µ–Ї—В—А–Њ–љ–љ–Њ–є –њ–Њ—З—В–µ

—А—Г—Б—Б–Ї–Є–є

–°–≤—П–ґ–Є—В–µ—Б—М —Б –љ–∞–Љ–Є –њ–Њ —Н–ї–µ–Ї—В—А–Њ–љ–љ–Њ–є –њ–Њ—З—В–µ
1. –Т–≤–µ–і–µ–љ–Є–µ
–С–Њ–ї—М—И–Є–µ –≤–Є–±—А–∞—Ж–Є–Њ–љ–љ—Л–є –≥—А–Њ—Е–Њ—В —И–Є—А–Њ–Ї–Њ –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –і–ї—П –≥—А–Њ—Е–Њ—З–µ–љ–Є—П, –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є–Є –Є –Њ–±–µ–Ј–≤–Њ–ґ–Є–≤–∞–љ–Є—П –≤ –≥–Њ—А–љ–Њ–і–Њ–±—Л–≤–∞—О—Й–µ–є –њ—А–Њ–Љ—Л—И–ї–µ–љ–љ–Њ—Б—В–Є, –Љ–µ—В–∞–ї–ї—Г—А–≥–Є–Є –Є —Е–Є–Љ–Є—З–µ—Б–Ї–Њ–є –њ—А–Њ–Љ—Л—И–ї–µ–љ–љ–Њ—Б—В–Є [1-3]. –Т –њ—А–Њ—Ж–µ—Б—Б–µ —А–∞–±–Њ—В—Л –ї—Г—З –≤–Є–±—А–∞—Ж–Є–Њ–љ–љ–Њ–≥–Њ –≥—А–Њ—Е–Њ—В–∞ –Ј–∞–≤–Є—Б–Є—В –Њ—В —З–∞—Б—В–Є—Ж —А–ґ–∞–≤—З–Є–љ—Л –Є —И–ї–∞–Љ–∞ –≤–Њ–і—Л, –Ї–Њ—В–Њ—А—Л–µ –њ—А–Є–≤–Њ–і—П—В –Ї —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–Љ—Г —А–∞–Ј—А—Г—И–µ–љ–Є—О –±–∞–ї–Ї–Є –Є –њ—А–Є–Њ—Б—В–∞–љ–Њ–≤–Є–ї –њ—А–Њ–Є–Ј–≤–Њ–і—Б—В–≤–Њ [4]. –Х—Б–ї–Є —Г—Б—В–∞–ї–Њ—Б—В–љ–∞—П —В—А–µ—Й–Є–љ–∞ –ї—Г—З–∞ –і–Є–∞–≥–љ–Њ—Б—В–Є—А—Г–µ—В—Б—П –Є —Г—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –±–∞–ї–Ї–Є –њ–Њ –њ—А–Њ–≥–љ–Њ–Ј–∞–Љ, –њ—А–Њ–Є–Ј–≤–Њ–і—Б—В–≤–µ–љ–љ–Њ–≥–Њ —В—А–∞–≤–Љ–∞—В–Є–Ј–Љ–∞ –Є —Н–Ї–Њ–љ–Њ–Љ–Є—З–µ—Б–Ї–Є—Е –њ–Њ—В–µ—А—М –Љ–Њ–ґ–љ–Њ –±—Л–ї–Њ –±—Л –Є–Ј–±–µ–ґ–∞—В—М. –®—В–∞–Љ–Љ –Љ–Њ–і–∞–ї—М–љ—Л–µ –њ–∞—А–∞–Љ–µ—В—А—Л –±–Њ–ї–µ–µ —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ—Л –Ї —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л, —З–µ–Љ —Б–Љ–µ—Й–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ [5], —В–∞–Ї –љ–∞–њ—А—П–≥–∞—В—М—Б—П –Љ–Њ–і–∞–ї—М–љ—Л–є –∞–љ–∞–ї–Є–Ј –Є—Б–њ–Њ–ї—М–Ј—Г–µ—В—Б—П –і–ї—П –≤—Л—П–≤–ї–µ–љ–Є—П –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –љ–∞ –≤–Є–±—А–Њ—А–µ–є–Ї–Є —Н–Ї—А–∞–љ–µ. Adewuyi –Є –Т—Г –Є—Б–њ–Њ–ї—М–Ј—Г—О—В—Б—П –Љ–Њ–і–∞–ї—М–љ—Л–µ –Љ–∞–Ї—А–Њ-–і–µ—Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –Љ–µ—В–Њ–і–Њ–≤ –≥–Є–±–Ї–Њ—Б—В—М –і–ї—П –ї–Њ–Ї–∞–ї–Є–Ј–∞—Ж–Є–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –≤ –Є–Ј–≥–Є–±–∞–µ–Љ—Л—Е –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–є [6]. –Ю–љ —Б–Њ–∞–≤—В. –њ—А–µ–і–ї–Њ–ґ–µ–љ –Љ–µ—В–Њ–і, –Ї–Њ—В–Њ—А—Л–є —В—А–µ–±—Г–µ—В –љ–Є–Ј–Ї–Њ—З–∞—Б—В–Њ—В–љ–Њ–≥–Њ —А–µ–ґ–Є–Љ–∞ –Є –љ–µ —В—А–µ–±—Г–µ—В –Љ–∞—Б—Б–Њ–≤–Њ–≥–Њ –љ–Њ—А–Љ–∞–ї–Є–Ј–∞—Ж–Є–Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, —З—В–Њ –і–µ–ї–∞–µ—В –Љ–µ—В–Њ–і –њ—А–Є–≥–Њ–і–љ—Л–Љ –і–ї—П –љ–µ—А–∞–Ј—А—Г—И–∞—О—Й–µ–≥–Њ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–≥–Њ –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Б—В—А—Г–Ї—В—Г—А –њ—А–Є –≤–Њ–Ј–±—Г–ґ–і–µ–љ–Є–Є –Њ–Ї—А—Г–ґ–∞—О—Й–µ–є —Б—А–µ–і—Л [7]. –Ґ—П –Є Buyukozturk –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞—В—М –Љ–Њ–і–∞–ї—М–љ—Л–µ —Н–љ–µ—А–≥–Є–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –≤ –Ї–∞—З–µ—Б—В–≤–µ –Є–љ–і–µ–Ї—Б–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –≤ –Љ–Њ–љ–Є—В–Њ—А–Є–љ–≥ —Б–Њ—Б—В–Њ—П–љ–Є—П –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–Є –Є –њ—А–µ–і–ї–∞–≥–∞–µ–Љ–Њ–є –≥–Є–±—А–Є–і–љ–Њ–є –Љ–љ–Њ–≥–Њ–Ї—А–Є—В–µ—А–Є–∞–ї—М–љ–Њ–є –Њ–њ—В–Є–Љ–Є–Ј–∞—Ж–Є–Є –∞–ї–≥–Њ—А–Є—В–Љ–Њ–≤ –і–ї—П –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –Љ–µ–ї–Ї–Є—Е –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –≤ —А–∞–Ј–ї–Є—З–љ—Л—Е —В—А–µ—Е–Љ–µ—А–љ—Л—Е —Б—В–∞–ї—М–љ—Л—Е –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–є [8]. –Т —Н—В–Њ–Љ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–Є, –Љ—Л –њ–Њ—Б—В—А–Њ–Є–ї–Є —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ–є –Є –љ–∞–і–µ–ґ–љ—Л–є –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М —Б–Њ—Б—В–Њ—П–љ–Є—П –≤–Є–±—А–Њ—А–µ–є–Ї–Є —Н–Ї—А–∞–љ –љ–∞ –Њ—Б–љ–Њ–≤–µ —И—В–∞–Љ–Љ–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, –Ї–Њ—В–Њ—А—Л–є –Љ–Њ–ґ–µ—В –њ—А–µ–і—Б–Ї–∞–Ј–∞—В—М –њ–Њ–≤—А–µ–ґ–і–µ–љ —Б—В–µ–њ–µ–љ–Є –Є –ї–Њ–Ї–∞–ї–Є–Ј–∞—Ж–Є–Є –њ—Г—З–Ї–∞. –Ч–∞—В–µ–Љ –њ–Њ –і–ї–Є–љ–µ —Г—Б—В–∞–ї–Њ—Б—В–љ–∞—П —В—А–µ—Й–Є–љ–∞, —Г—Б—В–∞–ї–Њ—Б—В–љ–∞—П —В—А–µ—Й–Є–љ–∞ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є—П –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ–Љ–Њ–≥–Њ –Я–∞—А–Є–ґ—Б–Ї–Њ–≥–Њ –Ј–∞–Ї–Њ–љ–∞.
2. –Ґ–µ–Њ—А–Є—П –Є–і–µ–љ—В–Є—Д–Є–Ї–∞—Ж–Є—П –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –љ–∞ –Њ—Б–љ–Њ–≤–µ —И—В–∞–Љ–Љ–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞
–Т–Є–±—А–Є—А—Г—П —Н–Ї—А–∞–љ –Є–Љ–µ–µ—В –љ–µ—Б–Ї–Њ–ї—М–Ї–Њ —Б—В–µ–њ–µ–љ–µ–є —Б–≤–Њ–±–Њ–і—Л —Б–Є—Б—В–µ–Љ—Л, –±–µ—Б–њ–ї–∞—В–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Ї–Њ–ї–µ–±–∞–љ–Є–є: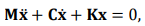 (1)
(1)
–≥–і–µ –Ь , –° –Є –Ъ –Љ–∞—Б—Б–∞, –і–µ–Љ–њ—Д–Є—А–Њ–≤–∞–љ–Є–µ –Є –ґ–µ—Б—В–Ї–Њ—Б—В—М –Љ–∞—В—А–Є—Ж—Л, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ [9].
–Ю—В –≠–Ї–≤. (1) –Љ—Л –Љ–Њ–ґ–µ–Љ —Б–і–µ–ї–∞—В—М:
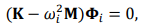 (2)
(2)
–≥–і–µ Wi-—Н—В–Њ ЁЕI-–Њ–є –Љ–Њ–і–∞–ї—М–љ–Њ–є —З–∞—Б—В–Њ—В—Л,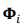 —П–≤–ї—П–µ—В—Б—П ЁЕ - –є —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є. –Я–Њ –і–∞–љ–љ—Л–Љ –Ї–Њ–љ–µ—З–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —В–µ–Њ—А–Є–Є, –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –њ—А–Њ—Ж–µ–і–Є—В–µ —А–µ–ґ–Є–Љ —Д–Њ—А–Љ—Л
—П–≤–ї—П–µ—В—Б—П ЁЕ - –є —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є. –Я–Њ –і–∞–љ–љ—Л–Љ –Ї–Њ–љ–µ—З–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ —В–µ–Њ—А–Є–Є, –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –њ—А–Њ—Ж–µ–і–Є—В–µ —А–µ–ґ–Є–Љ —Д–Њ—А–Љ—Л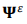 —Д–Њ—А–Љ—Л –Є —А–µ–ґ–Є–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є—П
—Д–Њ—А–Љ—Л –Є —А–µ–ґ–Є–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є—П 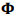 —Н—В–Њ:
—Н—В–Њ:
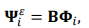 (3)
(3)
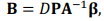 (4)
(4)
–≥–і–µ D-–ї–Є–љ–µ–є–љ—Л–є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–є –Њ–њ–µ—А–∞—В–Њ—А, –Я –Љ–∞—В—А–Є—Ж—Л —Д—Г–љ–Ї—Ж–Є—П —Б–Љ–µ—Й–µ–љ–Є—П, –Р —З–Є—Б–ї–µ–љ–љ–Њ–µ –Љ–∞—В—А–Є—Ж—Л,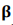 –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ –Љ–∞—В—А–Є—Ж—Л –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П [10].
–Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ –Љ–∞—В—А–Є—Ж—Л –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П [10].
–Ч–∞–Љ–µ–љ–Є—В—М –≠–Ї–≤. (3) –≤ –≠–Ш. (2), –Љ—Л –Љ–Њ–ґ–µ–Љ –њ–Њ–ї—Г—З–Є—В—М:
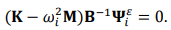 (5)
(5)
–Я–Њ –°—А–∞–≤–љ–µ–љ–Є—О –≠–Ї–≤. (2) –Є EQ. (5), —А–µ–ґ–Є–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є—П, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–Є–є —А–µ–ґ–Є–Љ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Є –Њ–±–∞ –Є–Љ–µ—О—В —В–µ –ґ–µ –Љ–Њ–і–∞–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л, –Љ–Њ–і–∞–ї—М–љ—Л–µ –Љ–Њ–і–∞–ї—М–љ—Л–µ –Љ–∞—Б—Б—Л –Є –ґ–µ—Б—В–Ї–Њ—Б—В–Є. –Ъ–Њ–≥–і–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –≤–Є–±—А–Є—А—Г—П —Н–Ї—А–∞–љ–∞ —Б–Њ–Ј–і–∞–µ—В —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л, –µ–µ –ґ–µ—Б—В–Ї–Њ—Б—В—М, —З–∞—Б—В–Њ—В–∞ –Є —Д–Њ—А–Љ–∞ –Ї–Њ–ї–µ–±–∞–љ–Є–є –Њ—В–ї–Є—З–∞–µ—В—Б—П –Њ—В –Є–љ—В–∞–Ї—В–љ–Њ–є —Б—В—А—Г–Ї—В—Г—А—Л, –Ї–Њ—В–Њ—А–∞—П:
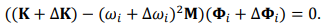 (6)
(6)
–°–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ, –љ–∞–њ—А—П–ґ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Є–Ј–Љ–µ–љ—П–µ—В—Б—П:
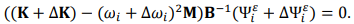 (7)
(7)
–†–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Є —Б—В–µ–њ–µ–љ–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –њ—А–µ–і—Б–Ї–∞–Ј–∞–љ–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ–Њ–є –ґ–µ—Б—В–Ї–Њ—Б—В–Є —В–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Є, –Љ–Њ–і–∞–ї—М–љ–Њ–є —З–∞—Б—В–Њ—В—Л –Є–ї–Є —А–µ–ґ–Є–Љ —Д–Њ—А–Љ—Л. –Э–∞ —Б–∞–Љ–Њ–Љ –і–µ–ї–µ, —Г—Б—В–∞–ї–Њ—Б—В—М, –њ–Њ–ї–Њ–Љ–Ї–Є –≤ –Њ—Б–љ–Њ–≤–љ–Њ–Љ –њ—А–Є–≤–Њ–і—П—В –Ї –ї–Њ–Ї–∞–ї—М–љ–Њ–є –ґ–µ—Б—В–Ї–Њ—Б—В–Є —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–љ—Л, –њ–Њ—Н—В–Њ–Љ—Г –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В –Є —А–µ–ґ–Є–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Љ–∞–ї–µ–љ—М–Ї–Є–µ, –∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –љ–∞–њ—А—П–ґ–µ–љ–Є—П —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –±–Њ–ї—М—И–Њ–є [11, 12]. –Т —Ж–µ–ї—П—Е –њ–Њ–≤—Л—И–µ–љ–Є—П —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ—Б—В–Є –Є –љ–∞–і–µ–ґ–љ–Њ—Б—В–Є —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –≤ —А–µ–Ј—Г–ї—М—В–∞—В–µ –і–Є–∞–≥–љ–Њ—Б—В–Є–Ї–Є, –Љ—Л —А–µ–Ї–Њ–Љ–µ–љ–і—Г–µ–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ—Л–µ –Є–Ј–Љ–µ–љ–µ–љ–Є—П (–°–†) –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П:
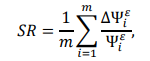 (8)
(8)
–≥–і–µ ЁЙ —П–≤–ї—П–µ—В—Б—П —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л–Љ –Ј–∞–Ї–∞–Ј—Л —А–µ–ґ–Є–Љ–µ.
3. –Я–µ—А–µ–Љ–µ—Й–µ–љ–Є–µ –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є—П –Љ–Њ–і–∞–ї—М–љ—Л–є –∞–љ–∞–ї–Є–Ј –≤–Є–±—А–Њ—А–µ–є–Ї–Є —Н–Ї—А–∞–љ
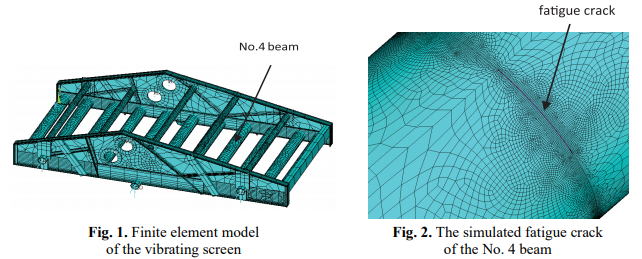
–Т —Н—В–Њ–є —Б—В–∞—В—М–µ –Љ—Л –≤—Л–±–Є—А–∞–µ–Љ 27 –Љ2 –±–Њ–ї—М—И–Њ–є –ї–Є–љ–µ–є–љ—Л–є –≤–Є–±—А–Є—А—Г—П —Н–Ї—А–∞–љ –≤ –Ї–∞—З–µ—Б—В–≤–µ –Њ–±—К–µ–Ї—В–∞ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П, –µ–≥–Њ –Ї–Њ–љ–µ—З–љ–Њ-—Н–ї–µ–Љ–µ–љ—В–љ–∞—П –Љ–Њ–і–µ–ї—М –њ–Њ–Ї–∞–Ј–∞–љ–∞ –љ–∞ —А–Є—Б. 1. –Ы—Г—З –≤–Є–±—А–Њ—Б–Є—В–Њ —Б—В—А—Г–Ї—В—Г—А–∞ —В—А—Г–±—З–∞—В–Њ–≥–Њ –њ—Г—З–Ї–∞, –µ–≥–Њ –≤–љ—Г—В—А–µ–љ–љ–Є–є –і–Є–∞–Љ–µ—В—А-300 –Љ–Љ, –Т–љ–µ—И–љ–Є–є –і–Є–∞–Љ–µ—В—А-320 –Љ–Љ, —В–Њ–ї—Й–Є–љ–∞-10 –Љ–Љ –Є –і–ї–Є–љ–∞ –ї—Г—З–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 3 600 –Љ–Љ. –Ь–∞—В–µ—А–Є–∞–ї –±–∞–ї–Ї–∞ 20 —Б—В–∞–ї—М —Г–≥–ї–µ—А–Њ–і–∞, –µ–≥–Њ –Љ–Њ–і—Г–ї—М —Г–њ—А—Г–≥–Њ—Б—В–Є —Б–Њ—Б—В–∞–≤–ї—П–µ—В 213 –≥–Я–∞, –њ–ї–Њ—В–љ–Њ—Б—В—М —Б–Њ—Б—В–∞–≤–ї—П–µ—В 7,8√Ч103 –Ї–≥/–Љ3 , –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Я—Г–∞—Б—Б–Њ–љ–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 0,28. –Я–Њ—В–Њ–Љ—Г —З—В–Њ –ї—Г—З-—Н—В–Њ —В–Њ–љ–Ї–Њ—Б—В–µ–љ–љ–∞—П –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є—П, –њ—А–Њ–±–Ї–∞, —Н–ї–µ–Љ–µ–љ—В SHELL181 –Њ–±–Њ–ї–Њ—З–Ї–∞ —Б —И–µ—Б—В—М—О —Б—В–µ–њ–µ–љ—П–Љ–Є —Б–≤–Њ–±–Њ–і—Л –Є 4 —Г–Ј–ї–Њ–≤ –±–Њ–ї–µ–µ –њ–Њ–і—Е–Њ–і–Є—В, —З–µ–Љ –±–∞–ї–Њ—З–љ—Л–є —Н–ї–µ–Љ–µ–љ—В –і–ї—П –Ї–Њ–љ–µ—З–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ [13].
–†–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л –љ–∞ –±–∞–ї–Ї–µ —З–∞—Б—В–Њ —Б–Њ–Ј–і–∞—О—В –љ–∞ —Б–µ—А–µ–і–Є–љ–µ –Є —З–µ—В–≤–µ—А—В–Є –њ—Г—З–Ї–∞, –њ–Њ—Н—В–Њ–Љ—Г –Љ–µ—Б—В–∞ —Г—Б–ї–Њ–≤–љ–Њ–є —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—О—В—Б—П –≤ —Б–µ—А–µ–і–Є–љ–µ –Є —З–µ—В–≤–µ—А—В–Є вДЦ 4 –Њ—В –ї—Г—З–∞ –≤ –Љ–Њ–і–µ–ї–Є –Ь–Ъ–≠. –£—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П –њ–µ—А—Д–Њ—А–∞—Ж–Є—П –њ–Њ–њ–µ—А–µ—З–љ–Њ–є —В—А–µ—Й–Є–љ–Њ–є —Б —И–Є—А–Є–љ–Њ–є 1 –Љ–Љ, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б. 2 [14, 15].
–Ы—Г—З –≤–Є–±—А–Є—А—Г—П —Н–Ї—А–∞–љ –Є–Љ–µ–µ—В —В—А—Г–±—З–∞—В–Њ–µ —Б—В—А–Њ–µ–љ–Є–µ, –њ–Њ—Н—В–Њ–Љ—Г —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л —П–≤–ї—П–µ—В—Б—П —В–Є–њ —В—А–µ—Й–Є–љ—Л –Њ–±–Њ–ї–Њ—З–Ї–Є. –Ъ—А–Є—В–Є—З–µ—Б–Ї–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л –њ—Г—З–Ї–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л—З–Є—Б–ї–µ–љ–∞ –њ–Њ —Г—А–∞–≤–љ–µ–љ–Є—О. (9):
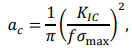 (9)
(9)
–≥–і–µ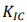 —Н—В–Њ —В—А–µ—Й–Є–љ–Њ—Б—В–Њ–є–Ї–Њ—Б—В–Є, F —П–≤–ї—П–µ—В—Б—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —Д–∞–Ї—В–Њ—А–Њ–Љ,
—Н—В–Њ —В—А–µ—Й–Є–љ–Њ—Б—В–Њ–є–Ї–Њ—Б—В–Є, F —П–≤–ї—П–µ—В—Б—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —Д–∞–Ї—В–Њ—А–Њ–Љ,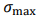 –Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є [16, 17]. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Љ–∞—В–µ—А–Є–∞–ї –±–∞–ї–Ї–Є 20 —Г–≥–ї–µ—А–Њ–і–Є—Б—В–∞—П —Б—В–∞–ї—М,
–Љ–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е –љ–∞–њ—А—П–ґ–µ–љ–Є–є [16, 17]. –Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –Љ–∞—В–µ—А–Є–∞–ї –±–∞–ї–Ї–Є 20 —Г–≥–ї–µ—А–Њ–і–Є—Б—В–∞—П —Б—В–∞–ї—М,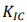 = 104 –Ь–Я–∞¬Ј–Ь1/2, ЁВ—Д= 1.5,
= 104 –Ь–Я–∞¬Ј–Ь1/2, ЁВ—Д= 1.5,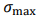 = 60 –Ь–Я–∞. –Ї—А–Є—В–Є—З–µ—Б–Ї–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л №љ
= 60 –Ь–Я–∞. –Ї—А–Є—В–Є—З–µ—Б–Ї–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л №љ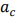 —А–∞–≤–љ–∞ 425 –Љ–Љ. –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞—В—М –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ –љ–∞–њ—А—П–ґ–µ–љ–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –Љ–µ–љ—П—В—М—Б—П –Є —Г—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –њ—Г—З–Ї–∞, —Б–Љ–µ—Й–µ–љ–Є–µ –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –±—Л–ї–Є —А–∞—Б—Б—З–Є—В–∞–љ—Л –њ–Њ 10 % –і–Њ 90 % –Њ—В –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–Ј–Љ–µ—А–∞ —В—А–µ—Й–Є–љ—Л, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ (—В. –µ. –ї—Г—З —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–≥–Њ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Б—В–µ–њ–µ–љ–Є). –Ы—Г—З –±—Л–ї –≤ –Ј–∞—Ж–µ–њ–ї–µ–љ–Є–Є —Б —Н–ї–µ–Љ–µ–љ—В–∞ SHELL181, –Ї–Њ—В–Њ—А—Л–є 12950 —Г–Ј–ї–Њ–≤ –Є —Н–ї–µ–Љ–µ–љ—В–Њ–≤ 12884. –С–ї–Њ—З–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ –Ы–∞–љ—Ж–Њ—И–∞ –±—Л–ї –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ –і–ї—П –Є–Ј–≤–ї–µ—З–µ–љ–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, –њ–µ—А–≤—Л–µ –њ—П—В—М –Љ–Њ–і–∞–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В –Є–љ—В–∞–Ї—В–љ–Њ–є –Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–є –±–∞–ї–Ї–Є –њ–Њ–Ї–∞–Ј–∞–љ—Л –≤ –Ґ–∞–±–ї. 1, –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Л–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П
—А–∞–≤–љ–∞ 425 –Љ–Љ. –Ф–ї—П —В–Њ–≥–Њ, —З—В–Њ–±—Л –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞—В—М –≤–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ –љ–∞–њ—А—П–ґ–µ–љ–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –Љ–µ–љ—П—В—М—Б—П –Є —Г—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –њ—Г—З–Ї–∞, —Б–Љ–µ—Й–µ–љ–Є–µ –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –±—Л–ї–Є —А–∞—Б—Б—З–Є—В–∞–љ—Л –њ–Њ 10 % –і–Њ 90 % –Њ—В –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–Ј–Љ–µ—А–∞ —В—А–µ—Й–Є–љ—Л, —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ (—В. –µ. –ї—Г—З —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–≥–Њ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Б—В–µ–њ–µ–љ–Є). –Ы—Г—З –±—Л–ї –≤ –Ј–∞—Ж–µ–њ–ї–µ–љ–Є–Є —Б —Н–ї–µ–Љ–µ–љ—В–∞ SHELL181, –Ї–Њ—В–Њ—А—Л–є 12950 —Г–Ј–ї–Њ–≤ –Є —Н–ї–µ–Љ–µ–љ—В–Њ–≤ 12884. –С–ї–Њ—З–љ—Л–Љ –Љ–µ—В–Њ–і–Њ–Љ –Ы–∞–љ—Ж–Њ—И–∞ –±—Л–ї –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ –і–ї—П –Є–Ј–≤–ї–µ—З–µ–љ–Є—П –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤, –њ–µ—А–≤—Л–µ –њ—П—В—М –Љ–Њ–і–∞–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В –Є–љ—В–∞–Ї—В–љ–Њ–є –Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–є –±–∞–ї–Ї–Є –њ–Њ–Ї–∞–Ј–∞–љ—Л –≤ –Ґ–∞–±–ї. 1, –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ—Л–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П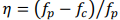 . –Ь–Њ–і–∞–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–≥–Њ —Г–Љ–µ–љ—М—И–Є—В—М –њ—Г—З–Ї–∞ –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–љ—В–∞–Ї—В–љ—Л–Љ–Є –ї—Г—З–∞, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤ –Ґ–∞–±–ї–Є—Ж–µ 1. –Я—А–Є—З–Є–љ–∞ —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л –≤—Л–Ј–≤–∞–ї–Њ —Г–Љ–µ–љ—М—И–µ–љ–Є–µ –ґ–µ—Б—В–Ї–Њ—Б—В–Є –Ј–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ—Л–є –ї—Г—З, –љ–Њ –Љ–∞—Б—Б–∞ –Њ—Б—В–∞–µ—В—Б—П –њ—А–µ–ґ–љ–µ–є –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–љ—В–∞–Ї—В–љ—Л–Љ–Є –ї—Г—З–∞, –њ–Њ —Н–Ї–≤. (2), –Љ–Њ–і–∞–ї—М–љ–Њ–є —З–∞—Б—В–Њ—В—Л –і–Њ–ї–ґ–љ—Л –±—Л—В—М —Г–Љ–µ–љ—М—И–µ–љ—Л. –Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ–∞—П —З–∞—Б—В–Њ—В–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 4.06 % –і–Њ –Є –њ–Њ—Б–ї–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П. –Т –Ї–∞—З–µ—Б—В–≤–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В, –Њ—З–µ–≤–Є–і–љ–Њ, –љ–µ –Є–Ј–Љ–µ–љ–Є—В—Б—П –і–Њ –Є –њ–Њ—Б–ї–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П, –Є—Б–њ–Њ–ї—М–Ј—Г—П –Љ–Њ–і–∞–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –љ–µ —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –Є —Б–ї–Њ–ґ–љ–Њ —Б—Г–і–Є—В—М –Њ –Љ–µ—Б—В–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П.
. –Ь–Њ–і–∞–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–≥–Њ —Г–Љ–µ–љ—М—И–Є—В—М –њ—Г—З–Ї–∞ –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–љ—В–∞–Ї—В–љ—Л–Љ–Є –ї—Г—З–∞, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤ –Ґ–∞–±–ї–Є—Ж–µ 1. –Я—А–Є—З–Є–љ–∞ —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л –≤—Л–Ј–≤–∞–ї–Њ —Г–Љ–µ–љ—М—И–µ–љ–Є–µ –ґ–µ—Б—В–Ї–Њ—Б—В–Є –Ј–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ—Л–є –ї—Г—З, –љ–Њ –Љ–∞—Б—Б–∞ –Њ—Б—В–∞–µ—В—Б—П –њ—А–µ–ґ–љ–µ–є –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–љ—В–∞–Ї—В–љ—Л–Љ–Є –ї—Г—З–∞, –њ–Њ —Н–Ї–≤. (2), –Љ–Њ–і–∞–ї—М–љ–Њ–є —З–∞—Б—В–Њ—В—Л –і–Њ–ї–ґ–љ—Л –±—Л—В—М —Г–Љ–µ–љ—М—И–µ–љ—Л. –Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–Њ–µ –Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ–∞—П —З–∞—Б—В–Њ—В–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В 4.06 % –і–Њ –Є –њ–Њ—Б–ї–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П. –Т –Ї–∞—З–µ—Б—В–≤–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е —З–∞—Б—В–Њ—В, –Њ—З–µ–≤–Є–і–љ–Њ, –љ–µ –Є–Ј–Љ–µ–љ–Є—В—Б—П –і–Њ –Є –њ–Њ—Б–ї–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П, –Є—Б–њ–Њ–ї—М–Ј—Г—П –Љ–Њ–і–∞–ї—М–љ—Л–µ —З–∞—Б—В–Њ—В—Л –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –љ–µ —Н—Д—Д–µ–Ї—В–Є–≤–љ–Њ –Є —Б–ї–Њ–ґ–љ–Њ —Б—Г–і–Є—В—М –Њ –Љ–µ—Б—В–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П.
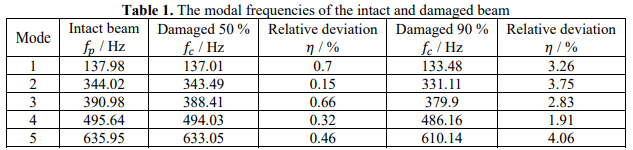
–°–Љ–µ—Й–µ–љ–Є—П –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ –Ї–Њ–љ–µ—З–љ–Њ-—Н–ї–µ–Љ–µ–љ—В–љ–Њ–є –Љ–Њ–і–µ–ї–Є –±—Л–ї–Є —А–∞—Б—Б—З–Є—В–∞–љ—Л, –њ–µ—А–≤–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ —Д–Њ—А–Љ—Л –≤–Њ–і–Њ–Є–Ј–Љ–µ—Й–∞—О—Й–µ–Љ —А–µ–ґ–Є–Љ–µ –њ–Њ–Ї–∞–Ј–∞–љ–∞ –љ–∞ —А–Є—Б. 3(–∞), –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —Д–Њ—А–Љ –Ї–Њ–ї–µ–±–∞–љ–Є–є –њ–Њ–Ї–∞–Ј–∞–љ—Л –љ–∞ —А–Є—Б. 3(–С), –Ї–Њ–≥–і–∞ –ї—Г—З –њ–Њ–≤—А–µ–ґ–і–µ–љ–Њ 60 –њ—А–Њ—Ж–µ–љ—В–Њ–≤. –Ь–∞–Ї—Б–Є–Љ–∞–ї—М–љ–∞—П –∞–Љ–њ–ї–Є—В—Г–і–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–µ –љ–∞–њ—А—П–ґ–µ–љ–Є–µ —Б–Њ–Ј–і–∞–µ—В –љ–∞ –њ–Њ–ї–њ—Г—В–Є –≤–і–Њ–ї—М –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П –і–ї–Є–љ—Л –њ—Г—З–Ї–∞ –Є–Ј-–Ј–∞ —Г—Б—В–∞–ї–Њ—Б—В–Є —Б—Г—Й–µ—Б—В–≤–Њ–≤–∞–љ–Є—П —В—А–µ—Й–Є–љ—Л.
–° –†–Є—Б. 3-—Н—В–Њ –Ї–Њ–љ—В—Г—А–љ–Њ–µ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ, —З—В–Њ –љ–µ—Г–і–Њ–±–љ–Њ –і–ї—П –Ї–Њ–ї–Є—З–µ—Б—В–≤–µ–љ–љ–Њ–є –Њ—Ж–µ–љ–Ї–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ—Л–µ –Ї—Г—А—Б –Љ–µ–љ—П–µ—В—Б—П, –њ–Њ—Н—В–Њ–Љ—Г –Љ—Л –≤—Л–±—А–∞–ї–Є –Њ–±—А–∞–Ј—Г—О—Й–µ–є –≤–і–Њ–ї—М –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П –і–ї–Є–љ—Л –±–∞–ї–Ї–Є –Є –њ—А–Њ–∞–љ–∞–ї–Є–Ј–Є—А–Њ–≤–∞–љ—Л –љ–∞–њ—А—П–≥–∞—О—В –Љ–Њ–і–∞–ї—М–љ—Л–µ —В–µ–љ–і–µ–љ—Ж–Є—П –Є–Ј–Љ–µ–љ–µ–љ–Є—П –њ–Њ –і–ї–Є–љ–µ –±–∞–ї–Ї–Є. –Ъ–Њ–≥–і–∞ –ї—Г—З —Б—В–µ–њ–µ–љ—М —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–≥–Њ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Б–Њ—Б—В–∞–≤–ї—П–µ—В 30%, –њ–µ—А–≤—Л–µ 3 —Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є–є –њ–Њ–Ї–∞–Ј–∞–љ—Л –љ–∞ —А–Є—Б. 4. –†–Є—Б. 4(–∞) —Д–Њ—А–Љ–∞ –≤–Њ–і–Њ–Є–Ј–Љ–µ—Й–∞—О—Й–µ–Љ —А–µ–ґ–Є–Љ–µ, –Ї–Њ—В–Њ—А–∞—П –љ–µ –≤–Є–і–љ–∞ –Љ—Г—В–∞—Ж–Є—П, –Ї–Њ–≥–і–∞ –ї—Г—З –≥–µ–љ–µ—А–Є—А–Њ–≤–∞—В—М —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л, —А–Є—Б. 4(–С) —А–µ–ґ–Є–Љ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —Д–Њ—А–Љ—Л, –Ї–Њ—В–Њ—А–∞—П –Є–Љ–µ–µ—В –њ–Є–Ї–Є –Љ—Г—В–∞—Ж–Є–Є –≤ —З–µ—В–≤–µ—А—В—М –Є —Б–µ—А–µ–і–Є–љ—Г –њ—Г—З–Ї–∞ –Є–Ј-–Ј–∞ —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л. –†–Є—Б. 4 –њ–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ —И—В–∞–Љ–Љ –Љ–Њ–і–∞–ї –њ–∞—А–∞–Љ–µ—В—А—Л –±–Њ–ї–µ–µ —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ—Л –Ї –њ–Њ–ї–Њ–Љ–Ї–µ, —З–µ–Љ —Б–Љ–µ—Й–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ–Њ —Н–Ї–≤. (8) –Љ—Л –≤—Л–±–Є—А–∞–µ–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ—Л–µ –Є–Ј–Љ–µ–љ–µ–љ–Є—П ( №µ №і ) –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞—В–µ–ї—М —Г—Й–µ—А–±–∞, –Ї–Њ—В–Њ—А—Л–є —П–≤–ї—П–µ—В—Б—П —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ—Л–Љ –Є —Н—Д—Д–µ–Ї—В–Є–≤–љ—Л–Љ.
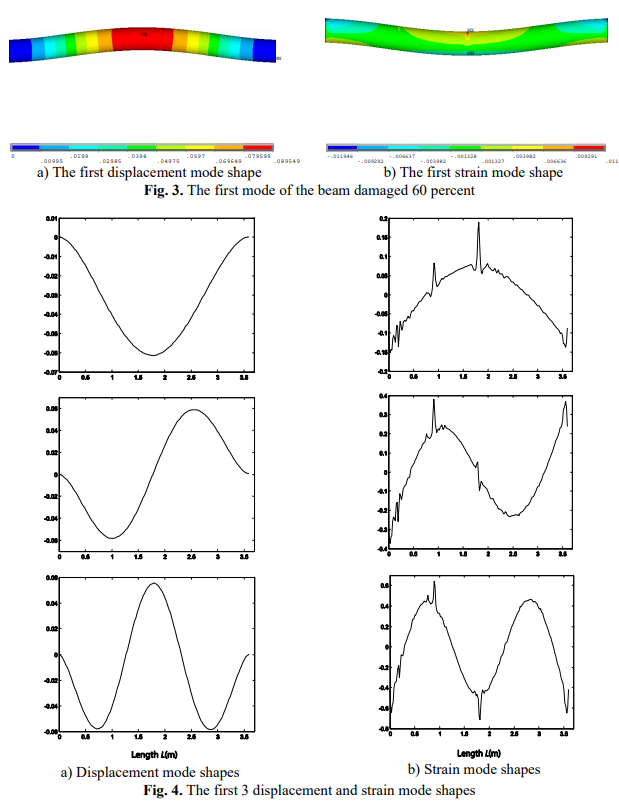
–°—А–∞–≤–љ–µ–љ–Є–µ —А–µ–ґ–Є–Љ–∞ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —Д–Њ—А–Љ—Л —Б —А–∞–Ј–ї–Є—З–љ–Њ–є —Б—В–µ–њ–µ–љ—М—О –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –њ–Њ–Ї–∞–Ј–∞–љ–∞ –љ–∞ —А–Є—Б. 5, —А–µ–ґ–Є–Љ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —Д–Њ—А–Љ—Л –≥–µ–љ–µ—А–Є—А–Њ–≤–∞—В—М –њ–Є–Ї –Љ—Г—В–∞—Ж–Є–Є –љ–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–µ –Љ–µ—Б—В–Њ. –Р–Љ–њ–ї–Є—В—Г–і—Л –њ–Є–Ї–∞ –Љ—Г—В–∞—Ж–Є–Є —Г–≤–µ–ї–Є—З–Є–≤–∞—О—В —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є —Г–≤–µ–ї–Є—З–Є–≤–∞–µ—В—Б—П –љ–∞ —З–µ—В–≤–µ—А—В—М –Є —Б–µ—А–µ–і–Є–љ–∞ –ї—Г—З–∞. –Я—А–Є—З–Є–љ–∞ —Б–Њ —Б—В–µ–њ–µ–љ—М—О –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Г–≤–µ–ї–Є—З–µ–љ–Є–µ –і–ї–Є–љ—Л —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–є —В—А–µ—Й–Є–љ—Л —А–∞—Б—И–Є—А—П—О—В, —З—В–Њ –њ—А–Є–≤–Њ–і–Є—В –Ї –ґ–µ—Б—В–Ї–Њ—Б—В–Є —Г–Љ–µ–љ—М—И–Є—В—М —Б–Њ—Б—В–∞–≤ –љ–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–µ –Љ–µ—Б—В–Њ. –®—В–∞–Љ–Љ —А–µ–ґ–Є–Љ–љ–Њ–µ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ —Б —А–∞–Ј–ї–Є—З–љ–Њ–є —Б—В–µ–њ–µ–љ—М—О –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –њ–Њ–Ї–∞–Ј–∞–љ—Л –љ–∞ —А–Є—Б. 6, –≤ —В–Њ–Љ —З–Є—Б–ї–µ –њ–µ—А–≤—Л—Е 3-—Е —А–µ–ґ–Є–Љ–Њ–≤ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Є –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤, —Б—В–Њ—А–Њ–љ–∞ –Ј–љ–∞—З–µ–љ–Є—П. –° –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–µ–Љ —Г–≤–µ–ї–Є—З–µ–љ–Є—П —Б—В–µ–њ–µ–љ–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–Њ–≤ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –≤–Њ–Ј—А–∞—Б—В–∞—О—В —Б –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ–є —В–µ–љ–і–µ–љ—Ж–Є–µ–є —Б—А–µ–і–Є —А–µ–ґ–Є–Љ–Њ–≤ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є. –Ъ–Њ–≥–і–∞ —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Б–Њ—Б—В–∞–≤–ї—П–µ—В –Љ–µ–љ–µ–µ 60 %, –љ–∞–њ—А—П–ґ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —Г–≤–µ–ї–Є—З–Є—В—Б—П —Б –Љ–µ–і–ї–µ–љ–љ–Њ–≥–Њ —Г—Б—В–Њ–є—З–Є–≤–Њ–≥–Њ —А–Њ—Б—В–∞, –љ–Њ –њ–Њ—Б–ї–µ —В–Њ–≥–Њ, –Ї–∞–Ї —Б—В–µ–њ–µ–љ—М —Г—Й–µ—А–±–∞ —Б–Њ—Б—В–∞–≤–ї—П–µ—В –±–Њ–ї–µ–µ 60 %, –љ–∞–њ—А—П–ґ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л–є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В —Г–≤–µ–ї–Є—З–µ–љ–Є—П –±—Л—Б—В—А–Њ–µ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–µ —В—А–µ—Й–Є–љ. –Т–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —Б—В–µ–њ–µ–љ—М—О –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Љ–Њ–≥—Г—В –±—Л—В—М —Г—Б—В–∞–љ–Њ–≤–ї–µ–љ—Л —Б –њ–Њ–Љ–Њ—Й—М—О –Љ–µ—В–Њ–і–∞ –љ–∞–Є–Љ–µ–љ—М—И–Є—Е –Ї–≤–∞–і—А–∞—В–Њ–≤, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤ —Г—А–∞–≤–љ–µ–љ–Є–Є. (10):
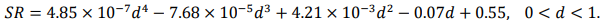 (10)
(10)
4. –£—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –≤–Є–±—А–Њ—А–µ–є–Ї–Є —Н–Ї—А–∞–љ
–Ц–Є–Ј–љ–Є —Г—Б—В–∞–ї–Њ—Б—В—М –≤–Є–±—А–Њ—А–µ–є–Ї–Є —Н–Ї—А–∞–љ–∞ –≤–Ї–ї—О—З–∞–µ—В –Є–љ–Є—Ж–Є–Є—А–Њ–≤–∞–љ–Є—П —В—А–µ—Й–Є–љ—Л –Ґ—А–µ—Й–Є–љ—Л –ґ–Є–Ј–љ–Є –Є –ґ–Є–Ј–љ–Є –ґ–Є–≤–Њ—В–љ—Л—Е. –Ъ–Њ–≥–і–∞ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є –љ–∞–њ—А—П–ґ–µ–љ–Є–є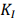 –±–Њ–ї—М—И–µ, —З–µ–Љ —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е —В—А–µ—Й–Є–љ –њ–Њ—А–Њ–≥
–±–Њ–ї—М—И–µ, —З–µ–Љ —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е —В—А–µ—Й–Є–љ –њ–Њ—А–Њ–≥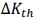 —В—А–µ—Й–Є–љ–∞ —А–Њ—Б—В –≤ —Б—В–∞–±–Є–ї—М–љ–Њ–є —Д–∞–Ј–µ, –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г —В—А–µ—Й–Є–љ —Б—В–∞–≤–Ї–∞
—В—А–µ—Й–Є–љ–∞ —А–Њ—Б—В –≤ —Б—В–∞–±–Є–ї—М–љ–Њ–є —Д–∞–Ј–µ, –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г —В—А–µ—Й–Є–љ —Б—В–∞–≤–Ї–∞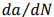 –Є
–Є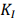 -–і–Є–∞–њ–∞–Ј–Њ–љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ ќФ
-–і–Є–∞–њ–∞–Ј–Њ–љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В–∞ ќФ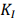 –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Я–∞—А–Є–ґ –Ј–∞–Ї–Њ–љ:
–Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Я–∞—А–Є–ґ –Ј–∞–Ї–Њ–љ:
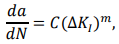 (11)
(11)
–≥–і–µ №љA-–і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л, №∞–Э - —З–Є—Б–ї–Њ —Ж–Є–Ї–ї–Њ–≤ –љ–∞–≥—А—Г–ґ–µ–љ–Є—П, —Б , –Љ-–Љ–∞—В–µ—А–Є–∞–ї—М–љ–∞—П –њ–Њ—Б—В–Њ—П–љ–љ–∞—П, c=2.11*10 -11 , –Љ=2.48:
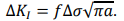 (12)
(12)
–Ч–∞–Љ–µ–љ–Є—В—М –≠–Ї–≤. (12) –≤ —Н–Ї–≤. (11) –Є –Ш–љ—В–µ–≥—А–∞–ї —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ—Л–є —А–µ—Б—Г—А—Б –Э –§ –Љ–Њ–ґ–љ–Њ —Б–і–µ–ї–∞—В—М –≤—Л–≤–Њ–і:
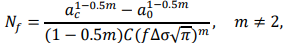 пЉИ13пЉЙ
пЉИ13пЉЙ
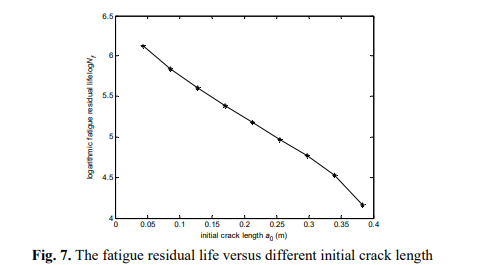
–≥–і–µ —Б –Ї—А–Є—В–Є—З–µ—Б–Ї–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л, –Э–Њ–ї—М —Н—В–Њ –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л, ЁВF —П–≤–ї—П–µ—В—Б—П –≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–Љ —Д–∞–Ї—В–Њ—А–Њ–Љ,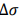 –љ–∞–њ—А—П–ґ–µ–љ–Є–µ –∞–Љ–њ–ї–Є—В—Г–і—Л [18]. –Т–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –љ–∞—З–∞–ї—М–љ–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л –Є –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Њ–є —Г—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–∞ –љ–∞ —А–Є—Б. 7, —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –љ–∞—З–∞–ї—М–љ–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ —Б–љ–Є–Ј–Є–ї–∞—Б—М. –Ъ–Њ–≥–і–∞ –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л —Б–Њ—Б—В–∞–≤–ї—П–µ—В –Љ–µ–љ–µ–µ 50 % –Њ—В –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ—Л–є —А–µ—Б—Г—А—Б –±—Л—Б—В—А–Њ —Б–љ–Є–ґ–∞–µ—В—Б—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–∞ –Њ—Б–љ–Њ–≤–µ —И—В–∞–Љ–Љ–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —И—В–∞–Љ–Љ–Њ–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Є —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л—А–∞–ґ–µ–љ–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ. (10), –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П, —В–Њ –Њ—В —Г—Б—В–∞–ї–Њ—Б—В–Є, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞—Б—Б—З–Є—В–∞–љ–∞ –њ–Њ —Г—А–∞–≤–љ–µ–љ–Є—О. (13).
–љ–∞–њ—А—П–ґ–µ–љ–Є–µ –∞–Љ–њ–ї–Є—В—Г–і—Л [18]. –Т–Ј–∞–Є–Љ–Њ—Б–≤—П–Ј—М –Љ–µ–ґ–і—Г –љ–∞—З–∞–ї—М–љ–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л –Є –ї–Њ–≥–∞—А–Є—Д–Љ–Є—З–µ—Б–Ї–Њ–є —Г—Б—В–∞–ї–Њ—Б—В—М –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–∞ –љ–∞ —А–Є—Б. 7, —Б —Г–≤–µ–ї–Є—З–µ–љ–Є–µ–Љ –љ–∞—З–∞–ї—М–љ–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ —Б–љ–Є–Ј–Є–ї–∞—Б—М. –Ъ–Њ–≥–і–∞ –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л —Б–Њ—Б—В–∞–≤–ї—П–µ—В –Љ–µ–љ–µ–µ 50 % –Њ—В –Ї—А–Є—В–Є—З–µ—Б–Ї–Њ–є –і–ї–Є–љ—Л —В—А–µ—Й–Є–љ—Л, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ—Л–є —А–µ—Б—Г—А—Б –±—Л—Б—В—А–Њ —Б–љ–Є–ґ–∞–µ—В—Б—П. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –љ–∞ –Њ—Б–љ–Њ–≤–µ —И—В–∞–Љ–Љ–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞, —Б–≤—П–Ј—М –Љ–µ–ґ–і—Г —И—В–∞–Љ–Љ–Њ–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є—П –Є —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Љ–Њ–ґ–µ—В –±—Л—В—М –≤—Л—А–∞–ґ–µ–љ–∞ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ. (10), –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л —Н–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ —Б—В–µ–њ–µ–љ—М –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П, —В–Њ –Њ—В —Г—Б—В–∞–ї–Њ—Б—В–Є, —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞—Б—Б—З–Є—В–∞–љ–∞ –њ–Њ —Г—А–∞–≤–љ–µ–љ–Є—О. (13).
5. –Т—Л–≤–Њ–і—Л
–Я–µ—А–µ–Љ–µ—Й–µ–љ–Є—П –Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ—Л–є –∞–љ–∞–ї–Є–Ј –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–≥–Њ –њ—Г—З–Ї–∞ –±—Л–ї–Є –њ—А–Њ–≤–µ–і–µ–љ—Л, —А–µ–Ј—Г–ї—М—В–∞—В—Л –њ–Њ–Ї–∞–Ј—Л–≤–∞—О—В, —З—В–Њ –Љ–Њ–і–∞–ї—М–љ—Л–µ –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П —З–∞—Б—В–Њ—В—Л –Њ—В –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–≥–Њ –њ—Г—З–Ї–∞ –Љ–∞–ї—Л –њ–Њ —Б—А–∞–≤–љ–µ–љ–Є—О —Б –Є–љ—В–∞–Ї—В–љ—Л–Љ–Є –ї—Г—З, —А–µ–ґ–Є–Љ –њ–µ—А–µ–Љ–µ—Й–µ–љ–Є—П —Д–Є–≥—Г—А—Л –Є–Љ–µ—О—В –љ–Є–Ї–∞–Ї–Є—Е –Њ—З–µ–≤–Є–і–љ—Л—Е –Є–Ј–Љ–µ–љ–µ–љ–Є–є —В–Њ—З–љ–Њ —В–∞–Ї –ґ–µ, –љ–Њ —А–µ–ґ–Є–Љ –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —Д–Њ—А–Љ—Л –њ–Є–Ї–Є –Љ—Г—В–∞—Ж–Є–Є –љ–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–љ–Њ–µ –Љ–µ—Б—В–Њ. –Ш–Ј –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ –Љ—Л –Њ–±–љ–∞—А—Г–ґ–Є–ї–Є, —З—В–Њ –њ—А–Є–µ–Љ –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Љ–Њ–і–∞–ї—М–љ–Њ–µ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Ї–∞–Ї –Є–љ–і–µ–Ї—Б–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –Є–Љ–µ–µ—В –њ—А–µ–Є–Љ—Г—Й–µ—Б—В–≤–∞ –Т—Л—Б–Њ–Ї–∞—П —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ–Њ—Б—В—М –Є —Е–Њ—А–Њ—И–∞—П –љ–∞–і–µ–ґ–љ–Њ—Б—В—М. –Ъ–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є —А–µ–ґ–Є–Љ–љ–Њ–µ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞—Б—Б—З–Є—В–∞–љ–Њ –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В —Б—В–µ–њ–µ–љ–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –ї—Г—З, –Ј–∞—В–µ–Љ —Г—Б—В–∞–ї–Њ—Б—В—М —В—А–µ—Й–Є–љ –Њ—Б—В–∞—В–Њ—З–љ–Њ–≥–Њ —А–µ—Б—Г—А—Б–∞ –Љ–Њ–ґ–µ—В –±—Л—В—М —А–∞—Б—Б—З–Є—В–∞–љ–∞ –њ–Њ –њ–∞—А–Є–ґ—Б–Ї–Є–Љ –Ј–∞–Ї–Њ–љ, —Б–Њ–≥–ї–∞—Б–љ–Њ –љ–∞—З–∞–ї—М–љ–∞—П –і–ї–Є–љ–∞ —В—А–µ—Й–Є–љ—Л.
–°—Б—Л–ї–Ї–Є
[1] –Т. –Я. –Ъ–ї–Є—А–Є, –°–Є–љ–љ–Њ—В—В –Ф. –Ь., –Ь–Њ—А—А–Є—Б–Њ–љ –†. –Ф. —А–∞–Ј–і–µ–ї–µ–љ–Є–µ –њ—А–Њ–Є–Ј–≤–Њ–і–Є—В–µ–ї—М–љ–Њ—Б—В–Є –і–≤—Г—Е—Н—В–∞–ґ–љ—Л—Е –≥—А–Њ—Е–Њ—В—Л —В–Є–њ–∞ "–±–∞–љ–∞–љ" вАУ –І–∞—Б—В—М 1: –њ–Њ—В–Њ–Ї–∞ –Є —Б–µ–њ–∞—А–∞—Ж–Є–Є –і–ї—П —А–∞–Ј–љ—Л—Е —Г—Б–Ї–Њ—А–µ–љ–Є–є. –Я–Њ–ї–µ–Ј–љ—Л—Е –Ш—Б–Ї–Њ–њ–∞–µ–Љ—Л—Е, –Ь–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є—П, –Т—Л–њ. 22 2009,, –°. 1218-1229.
[2] –ѓ–љ—В–µ–Ї –Ф. –°., –Ъ–∞–Љ–∞—А–≥–Њ –•. –†. —Б—В—А—Г–Ї—В—Г—А–љ—Л–µ –≤–Є–±—А–∞—Ж–Є–Є –Ї–∞–Ї –Є—Б—В–Њ—З–љ–Є–Ї —И—Г–Љ–∞ –љ–∞ –≤–Є–±—А–Њ–≥—А–Њ—Е–Њ—В–∞—Е. –Р–°–Ь–≠ –Ь–µ–ґ–і—Г–љ–∞—А–Њ–і–љ—Л–є –Ї–Њ–љ–≥—А–µ—Б—Б –Љ–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є—П –Є –≤—Л—Б—В–∞–≤–Ї–∞, 2009 –≥., –°. 213-222.
[3] –Ы. –Ы. –І–ґ–∞–Њ, –Ы—О –°. –°., –Ф. –•. –ѓ–љ –≤–Є—А—В—Г–∞–ї—М–љ—Л–є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В –њ–Њ–Ї–∞–Ј—Л–≤–∞–µ—В –Њ–і–љ–Є–Љ –і–≤–Є–ґ–µ–љ–Є–µ–Љ —З–∞—Б—В–Є—Ж –≤ –ї–Є–љ–µ–є–љ–Њ –≤–Є–±—А–Њ—Б–Є—В–Њ –њ–∞–ї—Г–±–µ. –У–Њ—А–љ–Њ–є –љ–∞—Г–Ї–Є –Є —В–µ—Е–љ–Є–Ї–Є, –≤—Л–њ. 20, –≤—Л–њ—Г—Б–Ї 2, 2010, —Б. 276-280.
[4] –Я—Н–љ –Ы. –Я., –Ы—О –°. –°., –С. –њ–µ—Б–љ—П C., –Є —Б–Њ–∞–≤—В. –°–Њ–≤–µ—А—И–µ–љ—Б—В–≤–Њ–≤–∞–љ–Є–µ –њ—А–Њ–µ–Ї—В–Є—А–Њ–≤–∞–љ–Є—П –±–∞–ї–Њ—З–љ—Л—Е –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–є –≤ –±–Њ–ї—М—И–Є–µ –≤–Є–±—А–∞—Ж–Є–Њ–љ–љ—Л–µ —Н–Ї—А–∞–љ —Б —Г—З–µ—В–Њ–Љ –Є–Ј–≥–Є–±–∞ –Є —Б–ї—Г—З–∞–є–љ—Л—Е –Ї–Њ–ї–µ–±–∞–љ–Є–є. –Ц—Г—А–љ–∞–ї –¶–µ–љ—В—А–∞–ї—М–љ–Њ–є –Ѓ–ґ–љ–Њ–є —Г–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞, –≤—Л–њ. 22, –Т—Л–њ—Г—Б–Ї 9, 2015, —Б—В—А. 3380-3388.
[5] —П–Љ –Ы. –Э., —В. –Ы—О–љ –Я., –С. –Ф. –Ы–Є, –Є —Б–Њ–∞–≤—В. –Ґ–µ–Њ—А–µ—В–Є—З–µ—Б–Ї–Њ–µ –Є —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ –њ—А–Њ—Ж–µ–і–Є—В—М. –Ц—Г—А–љ–∞–ї –Ј–≤—Г–Ї–∞ –Є –≤–Є–±—А–∞—Ж–Є–Є, –Њ–±—К–µ–Љ. 191, –≤—Л–њ—Г—Б–Ї 2, 1996, —Б—В—А. 251-260.
[6] –Р. –Я. Adewuyi, –Т—Г –Ч. –°. –Љ–Њ–і–∞–ї—М–љ—Л–µ –Љ–∞–Ї—А–Њ-–і–µ—Д–Њ—А–Љ–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –Љ–µ—В–Њ–і–Њ–≤ –≥–Є–±–Ї–Њ—Б—В—М –і–ї—П –ї–Њ–Ї–∞–ї–Є–Ј–∞—Ж–Є–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –љ–∞ –Є–Ј–≥–Є–± —Б—В—А—Г–Ї—В—Г—А—Л, –Є—Б–њ–Њ–ї—М–Ј—Г—П –і–ї–Є–љ–љ—Л–є-–і–∞—В—З–Є–Ї –і–∞—В—З–Є–Ї–Є –Т–С–†. –°—В—А—Г–Ї—В—Г—А–љ—Л–є –Ї–Њ–љ—В—А–Њ–ї—М –Є –Љ–Њ–љ–Є—В–Њ—А–Є–љ–≥ –Ј–і–Њ—А–Њ–≤—М—П, —В. 18, –≤—Л–њ—Г—Б–Ї 3, 2011, —Б—В—А. 341-360.
[7] –Њ–љ –Ы. –Ш., –ї–Є–∞–љ –Ф–ґ., –Ь. –С. –Є–љ—В–µ–ї–ї–µ–Ї—В—Г–∞–ї—М–љ—Л–є —Г—Й–µ—А–± –Љ–µ—В–Њ–і–∞ –Є–і–µ–љ—В–Є—Д–Є–Ї–∞—Ж–Є–Є –і–ї—П –±–Њ–ї—М—И–Є—Е —Б—В—А—Г–Ї—В—Г—А –љ–∞ –Њ—Б–љ–Њ–≤–µ —И—В–∞–Љ–Љ –Љ–Њ–і–∞–ї—М–љ—Л—Е –њ–∞—А–∞–Љ–µ—В—А–Њ–≤. –Ц—Г—А–љ–∞–ї –Ї–Њ–љ—В—А–Њ–ї—П –≤–Є–±—А–∞—Ж–Є–Є –Є —Г–њ—А–∞–≤–ї–µ–љ–Є—П, —В–Њ–Љ. 20, –≤—Л–њ—Г—Б–Ї 12, 2013, —Б—В—А. 1783-1795.
[8] –Ѓ. –Ѓ. –І–∞, Buyukozturk –Ю. —Б—В—А—Г–Ї—В—Г—А–љ—Л–µ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П, –Њ–±–љ–∞—А—Г–ґ–µ–љ–Є—П, –Є—Б–њ–Њ–ї—М–Ј—Г—П –Љ–Њ–і–∞–ї—М–љ—Л–µ —Н–љ–µ—А–≥–Є–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є –Є –≥–Є–±—А–Є–і –Љ–љ–Њ–≥–Њ–Ї—А–Є—В–µ—А–Є–∞–ї—М–љ–Њ–є –Њ–њ—В–Є–Љ–Є–Ј–∞—Ж–Є–Є. –Р–≤—В–Њ–Љ–∞—В–Є–Ј–Є—А–Њ–≤–∞–љ–љ–Њ–µ –≥—А–∞–ґ–і–∞–љ—Б–Ї–Њ–≥–Њ –Є –Є–љ–ґ–µ–љ–µ—А–љ–∞—П –Є–љ—Д—А–∞—Б—В—А—Г–Ї—В—Г—А–∞, —В–Њ–Љ. 30, –Т—Л–њ—Г—Б–Ї 5, 2015, —Б—В—А. 347-358.
[9] –Т–∞–љ –Х. –Ѓ., –І–ґ–∞–љ –Ч. –†. –њ–Њ—Е–Њ–ґ–Є–µ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ—Л–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є—П –Є—Б–њ—Л—В–∞–љ–Є—П –Љ–Њ–і–µ–ї–Є –Є –њ—А–Њ—В–Њ—В–Є–њ–∞ –≤–Є–±—А–Њ—Б–Є—В–Њ. –Т–µ—Б—В–љ–Є–Ї –Љ–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є—П, –≤—Л–њ. 47, –≤—Л–њ—Г—Б–Ї 5, 2011, —Б—В—А. 101-105.
[10] –љ—Г –Ї—А–∞–љ–Є—З—Г –Ґ. –ѓ. SlaviƒН, Bolte≈Њar –Ь. —Б—А–∞–≤–љ–µ–љ–Є–µ –њ—А–Њ—Ж–µ–і–Є—В—М –Є –Ї–ї–∞—Б—Б–Є—З–µ—Б–Ї–Њ–≥–Њ —Н–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–∞–ї—М–љ–Њ–≥–Њ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞. –Ц—Г—А–љ–∞–ї –Ї–Њ–љ—В—А–Њ–ї—П –≤–Є–±—А–∞—Ж–Є–Є –Є —Г–њ—А–∞–≤–ї–µ–љ–Є—П, —В–Њ–Љ. 22, 2016, —Б. 371-381.
[11] –С. –Ф. –Ы–Є, –І–ґ–∞–љ –Ѓ. –†., –Ы–Њ –Ф–ґ. —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ –Љ–µ—В–Њ–і–∞ –Љ–Њ–і–∞–ї—М–љ–Њ–≥–Њ –∞–љ–∞–ї–Є–Ј–∞ –њ—А–Є –∞–љ–∞–ї–Є–Ј–µ –і–Є–љ–∞–Љ–Є—З–µ—Б–Ї–Њ–є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є/–њ–Њ–ї—П –љ–∞–њ—А—П–ґ–µ–љ–Є–є. –Ц—Г—А–љ–∞–ї –≤–Є–±—А–∞—Ж–Є–Є –Є —Г–і–∞—А–Њ–≤, –Њ–±—К–µ–Љ. 4, 1992, —Б—В—А. 15-22.
[12] –ї–Є –Ѓ. –Ѓ., –І–µ–љ–≥ –ї., –±–∞—В–∞—В –Ы. –•., –Є —Б–Њ–∞–≤—В. –Ю–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Љ–µ—Б—В–∞ –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П –і–ї—П –њ–ї–∞—Б—В–Є–љ—З–∞—В—Л—Е –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–є —Б –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ–Љ —З—Г–≤—Б—В–≤–Є—В–µ–ї—М–љ—Л–є —Г—А–Њ–љ –њ–Њ–Ї–∞–Ј–∞—В–µ–ї–Є: –љ–∞–њ—А—П–ґ–µ–љ–Є–µ –Љ–Њ–і–∞–ї—М–љ—Л–є –њ–Њ–і—Е–Њ–і. –Ъ–Њ–Љ–њ—М—О—В–µ—А—Л –Є —Б–Њ–Њ—А—Г–ґ–µ–љ–Є–є, –≤—Л–њ. 80, –≤—Л–њ—Г—Б–Ї 25 2002,, –°. 1881-1894.
[13] –°. –Є–љ–љ–Њ–≤–∞—Ж–Є–Њ–љ–љ—Л–µ —Б—В—А—Г–Ї—В—Г—А–љ—Л–µ —А–µ—И–µ–љ–Є—П Baragetti –і–ї—П —В—П–ґ–µ–ї–Њ–љ–∞–≥—А—Г–ґ–µ–љ–љ—Л—Е –≤–Є–±—А–Њ–≥—А–Њ—Е–Њ—В–Њ–≤. –Я–Њ–ї–µ–Ј–љ—Л—Е –Ш—Б–Ї–Њ–њ–∞–µ–Љ—Л—Е, –Ь–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є–µ, –Т—Л–њ. 84, 2015, —Б—В—А. 15-26.
[14] –≤–µ–љ—В–Є–ї—П—В–Њ—А –Ц. –Ы., –У—Г–Њ –•. –Ы. —З–Є—Б–ї–µ–љ–љ–Њ–µ –Љ–Њ–і–µ–ї–Є—А–Њ–≤–∞–љ–Є–µ —Г–њ—А—Г–≥–Њ–њ–ї–∞—Б—В–Є—З–µ—Б–Ї–Њ–≥–Њ –њ–Њ–≤–µ–і–µ–љ–Є—П —А–Њ—Б—В–∞ —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е —В—А–µ—Й–Є–љ. –Ц—Г—А–љ–∞–ї –Љ–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є—П, –≤—Л–њ. 51, –≤—Л–њ—Г—Б–Ї 10 2015, —Б. 33-40.
[15] –љ—О –Ц., –Ч. –•. –І–ґ—Г–љ, –І—Г –§. –Я. –Љ–µ—В–Њ–і –Є–і–µ–љ—В–Є—Д–Є–Ї–∞—Ж–Є–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є–є –≤ –±–∞–ї–Њ—З–љ—Л—Е –Љ–Њ—Б—В–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–µ –Љ–µ—В–Њ–і–∞ –Ї–Њ–љ–µ—З–љ—Л—Е —Н–ї–µ–Љ–µ–љ—В–Њ–≤ –Љ–Њ–і–µ–ї—М –Њ–±–љ–Њ–≤–ї–µ–љ–Є—П –Є –Љ–Њ–і–∞–ї—М–љ—Л–µ —Н–љ–µ—А–≥–Є–Є –і–µ—Д–Њ—А–Љ–∞—Ж–Є–Є. –Э–∞—Г–Ї–∞ –Ъ–Є—В–∞–є –Ґ–µ—Е–љ–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е –Э–∞—Г–Ї, –Т—Л–њ. 58, –Т–Њ–њ—А–Њ—Б 4, 2015, —Б—В—А. 701-711. [16] –ї. –І—Н–љ—М, –¶–∞–є –Ы. –•. –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–µ —А–Њ—Б—В–∞ —В—А–µ—Й–Є–љ—Л —Г—Б—В–∞–ї–Њ—Б—В–Є –њ–Њ–≤–µ–і–µ–љ–Є—П –Љ–∞—В–µ—А–Є–∞–ї–Њ–≤ —Б —Г—З–µ—В–Њ–Љ —Г—Б—В–∞–ї–Њ—Б—В–Є –њ–Њ–≤—А–µ–ґ–і–µ–љ–Є—П —Г –≤–µ—А—И–Є–љ—Л —В—А–µ—Й–Є–љ—Л. –Т–µ—Б—В–љ–Є–Ї –Љ–∞—И–Є–љ–Њ—Б—В—А–Њ–µ–љ–Є—П, –≤—Л–њ. 48, –≤—Л–њ—Г—Б–Ї 20, 2012, —Б—В—А. 51-56.
[17] –С–∞–є –•., –°–µ –Ы. –ѓ. —Г—Б—В–Њ–є—З–Є–≤—Л–µ —Б–ї—Г—З–∞–є–љ—Л–µ –љ–∞–≥—А—Г–Ј–Ї–Є –Љ–µ—В–Њ–і –њ—А–Њ–≥–љ–Њ–Ј–Є—А–Њ–≤–∞–љ–Є—П —Г—Б—В–∞–ї–Њ—Б—В–љ–Њ–≥–Њ —А–Њ—Б—В–∞ —В—А–µ—Й–Є–љ—Л –ґ–Є–Ј–љ–Є. –Р—Б—В–∞ –Р—Н—А–Њ–љ–∞—Г—В–Є–Ї–∞ –≠—В Astronautica –°–Є–љ–Є—Ж–∞, —В–Њ–Љ. 35, –≤—Л–њ—Г—Б–Ї 9, 2014, —Б—В—А. 2500-2505.
[18] –¶–µ—А–±—Б—В—Б–Ї–∞—П –£., Vormwald –Ь., Pippan —А., –Є —Б–Њ–∞–≤—В. –Ю–± —Г—Б—В–∞–ї–Њ—Б—В–љ—Л—Е —В—А–µ—Й–Є–љ –њ–Њ—А–Њ–≥ –Љ–µ—В–∞–ї–ї–Њ–≤ –≤ –Ї–∞—З–µ—Б—В–≤–µ –Ї—А–Є—В–µ—А–Є—П –і–Є–Ј–∞–є–љ вАУ –Њ–±–Ј–Њ—А. –Ш–љ–ґ–µ–љ–µ—А–љ–Њ–є –Ь–µ—Е–∞–љ–Є–Ї–Є –†–∞–Ј—А—Г—И–µ–љ–Є—П, –Ґ. 153, 2016, —Б. 190-243.
–њ–Њ–Ј–≤–Њ–љ–Є –љ–∞–Љ :
—Н–ї–µ–Ї—В—А–Њ–љ–љ–∞—П –њ–Њ—З—В–∞ : sales@vrvibratory.com –њ–Њ–і–і–µ—А–ґ–Є–≤–∞–µ—В—Б—П —Б–µ—В—М ipv6
–њ–Њ–і–і–µ—А–ґ–Є–≤–∞–µ—В—Б—П —Б–µ—В—М ipv6 